Player Position Estimation on the Court Using Homography Transformations

2. Understanding Homography and Its Applications

2.1 What is Homography?

Homography is the mathematical transformation that establishes correspondence between two views of the same planar surface from different viewpoints. It essentially represents a mapping of points in one image plane to another, under the assumption that two image planes capture the same flat surface. Most tasks involving computer vision require various camera viewpoint changes, where homography has been found extremely useful because it aids in aligning and matching corresponding points among images.

A 3x3 matrix encodes a homography transformation, denoted as H. This contains rotation, translation, scaling, and perspective distortion, so it allows mapping pixel coordinates from one image (say, a video frame) to another, say, a court or field model. Mathematically, for a point P=(x,y) in the image frame, its corresponding point P′=(X,Y) in the real-world plane is given by:

Here, H is the homography matrix that transforms the point from image space to real-world coordinates.

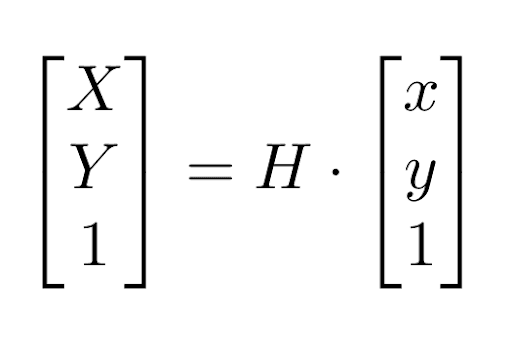
2.2 How Homography Works

Homography is founded on the assumption that a basketball court or a soccer field, among others, is a flat, planar surface. If various video frame points can correspond to positions known on the court, it will be possible to calculate the homography matrix. And with this calculated, it's quite straightforward to project any point in the image onto the real coordinate system of the court.
An important aspect of homography is that it makes lines straight but doesn't make angles or lengths the same. That characteristic alone makes homography ideal to map an angle-viewed image (since most sports footage is shot this way) onto a planar, bird's eye view of the court, where real measurements can be made.

2.3 Applications of Homography in Sports Analytics

Homography makes sports analytics incredibly powerful, because the player positions can be mapped from the video frames onto a known court layout with accuracy, thus opening up an extremely wide range of applications when analyzing games - both in real-time and off.

Player Position Estimation

The strongest application of homography in sports analytics is indeed the estimation of the position of a player. Homography can transform player coordinates in a 2D camera view into real-life court coordinates starting from video footage of the game. This transformation helps track the movement of players about the court very accurately and gives interesting insights to coaches and analysts about the player's positioning, spacing, and movement patterns.

Tactical and Strategic Analysis

By determining player positions using homography, access and insights into tactical analysis become much easier to achieve. Then, making projections onto a real-world court layout gives analysts an insight into how teams set up defensively, transition between phases of play, and how individual players fit into team formations.

Heatmaps and Trackings

Using homography-based transformations, sports teams can generate heat maps of player activity over a game. Such heat maps provide knowledge of the areas that are most occupied by the court or the field where individual players or the whole team spend most of their time. In doing so, coaches will be able to analyze player tendencies and check whether the players occupy the right zones during critical moments of the game.

Real-Time Player Tracking and Automation

Now, using advanced computer vision and machine learning, comes automation with the use of homography, where the tracking of a player can easily be automatically done in real-time. Such a system can automatically spot players in live video streams, estimate their positions on the field through homography, then provide real-time feedback to coaches and analysts. This means real-time tracking is invaluable for sports like basketball and soccer, wherein game outcomes can depend on fast decisions on player positionings.

Performance Metrics and Player Comparisons

Estimation of player positions in a very accurate way enables generation of multiple performance metrics, which are used to evaluate and compare the performances. Homography can transform the coordinates of the player from video to real world distance covered, sprint speed, and reaction time. All this data is put to use for comparison of players between games or improvement tracking or for understanding anomalies in their performance.

3. Challenges in Accurate Player Position Estimation

Although the homography transformation has many advantages, there are a number of issues that have to be addressed to make accurate estimation of player position feasible:

3.1 Camera Calibration Problem

In order to achieve an accurate estimate, camera calibration should be very accurate; it includes the removal of lens distortion, camera height variation, and perspective change. Poor camera calibration may result in extreme errors in the homography matrix obtained, which will finally produce erroneous positions of players.

3.2. Dynamic Movement of Cameras

Most sport recordings have panning, tilting, or zooming cameras, so the camera moves significantly throughout a game. Such camera movement introduces perspective changes that make it difficult to keep homography transformation constant for all the frames.

3.3. Player Occlusions and Overlaps

Homography is founded on the assumption that a basketball court or a soccer field, among others, is a flat, planar surface. If various video frame points can correspond to positions known on the court, it will be possible to calculate the homography matrix. And with this calculated, it's quite straightforward to project any point in the image onto the real coordinate system of the court.
An important aspect of homography is that it makes lines straight but doesn't make angles or lengths the same. That characteristic alone makes homography ideal to map an angle-viewed image (since most sports footage is shot this way) onto a planar, bird's eye view of the court, where real measurements can be made.

3.4 Propagation and Accumulation

The point correspondences may introduce small errors, and these propagated along the homography matrix will result in significant deviations in the real-world positions. These errors should be as low as possible during the computation of the matrix. The next sections will explain how thoughtful designs for and implementations of the transformation process that make use of homography will address these challenges.

4. Homography-Based Approach for Player Position Estimation

This step describes the homography transformations and spans data acquisition, matrix computation, and position mapping in an iterative approach for player-position estimation.

4.1 Data Acquisition and Preprocessing

4.1.1 Video Capture and Frame Extraction

Good quality video is captured through fixed or dynamic cameras. The frames are extracted at constant intervals so the court boundaries and reference points will be visible. If a dynamic camera is utilized, real-time frame extraction is done to capture the action during the actual game play.

4.1.2 Image Rectification and Calibration

The camera calibration removes the effects of barrel or pincushion distortion from the lens. The intrinsic and extrinsic parameters of the camera are determined using a calibration pattern like a checkerboard for removing geometric distortions before the homography matrix calculation.

4.2 Calculating the Homography Matrix

4.2.1 Identification of Correspondence Points

For determining the homography matrix, at least four non-collinear points should be determined both in the video frame or image plane and real court or reference plane. These points are determined manually or automatically through computer vision techniques like feature matching that involves Harris corners, SIFT, SURF.Commonly used points are:

• Court Corners
• Center circle points
• Important boundary intersections

4.2.2. Computing the Homography Matrix

The homography matrix H is calculated using the DLT method. Assuming that it has been provided with the corresponding points in the image and court, and (xi,yi) and (Xi,Yi)as the following relation describes:

4.3 Player Localization and Tracking

Players are located at all frames based on deep learning-based object detection algorithms YOLO (You Only Look Once). The location of the detected players are taken out as pixel coordinates xp,yp for each frame.

4.3.1 Object Detection

Deep learning models are employed to train the classification network so that each labeled image of a player is detected and localized in each frame. The marked bounding boxes on the players are used to calculate centroids to be able to track correctly.

4.3.2 Temporal Tracking

For an efficient tracking of the player, a unique and consistent ID is assigned for every detected player across frames. Employing algorithms such as Kalman filters, SORT (Simple Online and Realtime Tracking), or DeepSORT ensures that players get detected even in the presence of occlusions without errors.

4.4 Translating Player Positions to Real-World Coordinates

Once the positions of the players are detected in the image frame, the homography matrix H transforms the pixel coordinates into real court coordinates. The transformation is given by: Once this transformation has taken place, the homogeneous coordinates are normalized by dividing the Z-component and the mapping of the players to the correct position on the court is ensured.

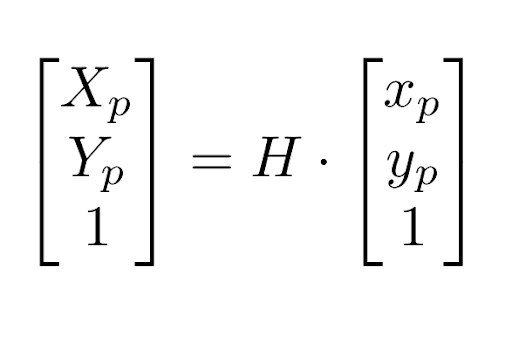
Where:

• (xp​,yp​) are the player's pixel coordinates.
• (Xp, Yp) are the corresponding court coordinates.

After applying the transformation,normalization of the Z-component requires the use of homogeneous coordinates, which must be transformed back into Cartesian coordinates in order to map the players accurately on the playing court.

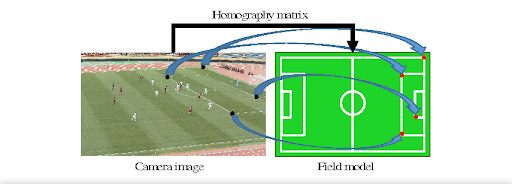
5. Verification and Validation

In order to assess the accuracy and efficiency of the proposed player position estimation technique based on homography transformations, two specific verification methods were applied. These methods focus on the verification of mapping accuracy of key regions in the video to the standard court model and checking the players' movement being confined inside specified Regions of Interest (ROI) in the video and the standard court model.

5.1 Key Region Mapping and Movement Translation

The method checks the validity of mapping important areas in the video to the standard court model and making valid player movements within those important areas. This approach enables you to determine that any transformation is valid and that player movements are preserved when mapped to the court model correctly.

Steps:

Identify Important Areas and Key Regions

Key areas in the video are determined based on significance in the game for example, the three-point arc in basketball, or penalty box in soccer.These regions are hand-annotated in the frames to be used as a reference point for comparison with the real court model.

Map Key Regions to Standard Court/Field Model

The identified regions from the video are then mapped onto the standard court model using the homography matrix so that the boundaries of those regions can be projected accurately onto the predefined court layout.

Translate Observed Movement

In the video, player movements are tracked in the above identified regions. Now, pixel positions of such movements are projected onto the court model using the same computed homography matrix onto similar areas. For example, if a player is detected to move inside three points in a basketball video, then his position will undergo transformation and would be projected onto the similar area in the real-world court model.

Check Mapping Correctness

The correctness of the transformation is checked by checking whether the motion captured of the players in the key regions of the video accurately projects to the same key region in the court model.The consistency of the key regions of the player before and after the transformation in the video and in the court model is verified with the help of a comparison of their positions

Evaluation Metrics

Mapping Accuracy. One applies mapping accuracy which measures the accuracy of how the positioning of the players in the video is transformed into the court model. This is measured in terms of Mean Squared Reprojection Error, referring to how much the difference between the positions in the video frame deviate from their projected positions in the court model.
This strategy verifies that regions of interest on the court are reflected between the video and virtual model, and also that the players' locations in regard to these regions are properly projected subsequent to applying transforms. In other words, evaluation of tactics about player location within these regions of interest areas is valid.

5.2 Region of Interest (ROI) Confinement and Heatmap Validation

Define a Region of Interest (ROI) for the movement of the player within the short video duration, such that the movement in the video stays within the ROI along both the video and the standard court model. Based on that, you then check if the movement heatmap of the player, computed over the standard court model, actually coincides with the same ROI defined within the video.

Steps:

Define the Region of Interest (ROI)

A Region of Interest (ROI) is manually defined within the video frame for a given period of play. The region chosen here is based on tactical relevance, such as defensive area in basketball or a half-court segment.The ROI area has definite boundaries. So the player will not cross boundaries during the analysis period.

Track Player Movement

The movement of the player inside the ROI is tracked all through the video clip. Object detection algorithms monitor the movement; the pixel coordinates of the player at every frame are captured to track their movement trajectory.

Create a Heatmap

A heatmap that depicts the movement of the player based on the movement within the defined boundaries of the ROI in a video frame, at the areas where the player has been most active and dense for movement will be shown.

Project ROI to Standard Court Model

Video player movement data is transformed by application of the homography matrix and projected onto the standard model of the court. A corresponding heatmap is generated in the real-world coordinate system for visualizing player movement.

Check Heatmap is Constrained:

The region of interest defined on the video is compared with the confines of the player's movement heatmap on the court model. The objective here is to check whether the movement of the player remains within the same region on both the video and the court model.The discrepancies between the confines of the heatmap on the video and the court model measure the accuracy of the transformation.

Evaluation Metrics:

Heatmap Confinement Accuracy or HCA: This HCA measures how well or accurately the player's movement in the video frame is constrained to be similar boundaries in the standard court model. That is, if a player's movement is strongly transformed and confined within a well-defined ROI on the court model, then a high HCA score is indicated.

6. Use Cases and Benefits

Tactical Analysis

The snapshot of player spatial positions achieved with sufficient resolution can be then used to demonstrate tactic formation, spacing, or individual player role.

Performance Evaluation

Real-space coordinates can be applied to measure the speed, acceleration, and movement economies of the players.

Create a Heatmap

A heatmap that depicts the movement of the player based on the movement within the defined boundaries of the ROI in a video frame, at the areas where the player has been most active and dense for movement will be shown.

Automated Video Annotation

This method can be included in video analysis software to enable automatic annotations of players and real-time updates on positions.

Enhanced Decision-Making

The positional data may be used to develop a predictive model for game results or to optimize strategies applied during the game.

7. Conclusion

This whitepaper outlined a general framework for the estimation of positions of players in a sports court environment that leveraged homography transformations. This provided the means for powerful tactical analysis and performance evaluation/strategic planning in sports analytics, by accurately mapping image-based positions of players onto a real-world coordinate system. This proposed method demonstrates robustness and accuracy on various sports scenarios and, thus, opens up advanced applications of sports analytics.

8. Future Enhancements

Real-time recalibration techniques to address camera panning and zooming, Dynamic Homography Recalibration Extensions to multi-camera setup for 3D position estimation, 3D Position Estimation Combination with sensor data, video-based tracking, increased accuracy and validation by combination with sensor data, for example, GPS. The basics of homography transformations: Understand the basic principles of homography and how it can be used in video-based mapping to real-world court coordinates of players.

9. What You Will Learn from This Whitepaper

• The fundamentals of homography transformations: Understand the basic principles of homography and how it can be used in video-based mapping to real-world court coordinates of players.
• Limitations in manual player tracking: Learn how the limitations of traditional manual tracking techniques are, in contrast to advantages seen in computer vision-based automated player tracking systems.
• Benefits of using homography in sports analytics: Learn how homography enhances tactical analysis, player movement tracking, and even decision-making during the live stream of sports.
• Key features of homography-based player tracking systems:Determine the technical demands of devising and implementing a player tracking system by applying homography transformations.
• Calculation of homography matrix: Understand how points are matched and calculated to translate video coordinates into real-world positions.
• Key takeaways from this whitepaper: How homography transformations change the landscape of sports analytics - accuracy, scalability, and automation of real-time and ex-post tracking of players.